15   Newer TCP Implementations

Since the rise of TCP Reno, several TCP alternatives to Reno have been developed; each attempts to address some perceived shortcoming of Reno. While many of them are very specific attempts to address the high-bandwidth problem we considered in 14.9   The High-Bandwidth TCP Problem, some focus primarily or entirely on other TCP Reno foibles. One such issue is TCP Reno’s “greediness” in terms of queue utilization; another is the lossy-link problem (14.10   The Lossy-Link TCP Problem) experienced by, say, Wi-Fi users.

Generally speaking, a TCP implementation can respond to congestion at the cliff – that is, it can respond to packet losses – or can respond to congestion at the knee – that is, it can detect the increase in RTT associated with the filling of the queue. These strategies are sometimes referred to as loss-based and delay-based, respectively; the latter term because of the rise in RTT. TCP implementers can tweak both the loss response – the multiplicative decrease of TCP Reno – and also the way TCP increases its cwnd in the absence of loss. There is a rich variety of options available.

The concept of monitoring the RTT to avoid congestion at the knee was first introduced in TCP Vegas (15.4   TCP Vegas). One striking feature of TCP Vegas is that, in the absence of competition, the queue may never fill, and thus there may not be any congestive losses. The TCP sawtooth, in other words, is not inevitable.

When losses do occur, most of the mechanisms reviewed here continue to use the TCP NewReno recovery strategy. As most of the implementations here are relatively recent, the senders can generally expect that the receiving end will support SACK TCP, which allows more rapid recovery from multiple losses.

On linux systems, the TCP congestion-control mechanism can be set by writing an appropriate string to /proc/sys/net/ipv4/tcp_congestion_control; the options on my system as of this writing are

• highspeed
• htcp
• hybla
• illinois
• vegas
• veno
• westwood
• bic
• cubic

We review several of these below. TCP Cubic is currently (2013) the default linux congestion-control implementation; TCP Bic was a precursor.

15.1   High-Bandwidth Desiderata

One goal of all TCP implementations that attempt to fix the high-bandwidth problem is to be unfair to TCP Reno: the whole point is to allow cwnd to increase more aggressively than is permitted by Reno. Beyond that, let us review what else a TCP version should do.

First is the backwards-compatibility constraint: any new TCP should exhibit reasonable fairness with TCP Reno at lower bandwidth×delay products. In particular, it should not ever have a significantly lower cwnd than a competing TCP Reno would get. But also it should not take bandwidth unfairly from a TCP Reno connection: the above comment about unfairness to Reno notwithstanding, the new TCP, when competing with TCP Reno, should leave the Reno connection with about the same bandwidth it would have if it were competing with another Reno connection. This is possible because at higher bandwidth×delay products TCP Reno does not efficiently use the available bandwidth; the new TCP should to the extent possible restrict itself to consuming this previously unavailable bandwidth rather than eating significantly into the bandwidth of a competing TCP Reno connection.

There is also the self-fairness issue: multiple connections using the new TCP should receive similar bandwidth allocations, at least with similar RTTs. For dissimilar RTTs, the bandwidth proportions should ideally be no worse than they would be under TCP Reno.

Ideally, we also want relatively rapid convergence to fairness; fairness is something of a hollow promise if only connections transferring more than a gigabyte will benefit from it. For TCP Reno, two connections halve the difference in their respective cwnds at each shared loss event; as we saw in 14.7.1   AIMD and Convergence to Fairness, slower convergence is possible.

It is harder to hope for fairness between competing new implementations. However, at the very least, if new implementations tcp1 and tcp2 are competing, then neither should get less than TCP Reno would get.

Some new TCPs make use of careful RTT measurements, and, as we shall see below, such measurements are subject to a considerable degree of noise. Any new TCP implementation should be reasonably robust in the face of inaccuracies in RTT measurement; a modest or transient measurement error should not make the protocol behave badly, in either the direction of low cwnd or of high.

Finally, a new TCP should ideally try to avoid clusters of multiple losses at each loss event. Such multiple losses, for example, are a problem for TCP NewReno without SACK: as we have seen, it takes one RTT to retransmit each lost packet. Even with SACK, multiple losses complicate recovery. Yet if a new TCP increments cwnd by an amount N>1 after each RTT, then there is potential for the network ceiling to be exceeded by N within one RTT, making a cluster of N losses reasonably likely to occur. These losses are likely distributed among all connections, not just the new-TCP one.

All TCPs addressing the high-bandwidth issue will need a cwnd-increment N that is fairly large, at least some of the time, apparently conflicting with this no-multiple-losses ideal. One trick is to reduce N when packet loss appears to be imminent. TCP Illinois and TCP Cubic do have mechanisms in place to reduce multiple losses.

15.2   RTTs

The exact performance of some of the faster TCPs we consider – for that matter, the exact performance of TCP Reno – is influenced by the RTT. This may affect individual TCP performance and also competition between different TCPs. For reference, here are a few typical RTTs from Chicago to various other places:

• US West Coast: 50-100 ms
• Europe: 100-150 ms
• Southeast Asia: 100-200 ms

15.3   Highspeed TCP

An early proposed fix for the high-bandwidth-TCP problem is HighSpeed TCP, documented in RFC 3649 (Floyd, 2003). Highspeed TCP is sometimes called HS-TCP, but we use the longer name here to avoid confusion with the entirely unrelated H-TCP, below.

For each loss-free RTT, Highspeed TCP allows a cwnd increment by more than 1.0, at least once cwnd is large enough. If the cwnd-increment value is N = N(cwnd), this is equivalent to having N parallel TCP Reno connections. Here are the cwnd-increment values in terms of cwnd:

cwnd	N(cwnd)
1	1.0
10	1.0
100	1.4
1,000	3.6
10,000	9.2
100,000	23.0

The formula for N(cwnd) is largely empirical; an algebraic expression for it is

N(cwnd) = max(1.0, 0.23×cwnd^0.4)

The second term in the max() above begins to dominate when cwnd = 38 or so.

It may be helpful to view Highspeed TCP in terms of the cwnd graph between losses. For ordinary TCP, the graph increases linearly. For Highspeed TCP, the graph is convex (lying above its tangent). This means that there is an increase in the rate of cwnd increase, as time goes on (up to the point of packet loss).

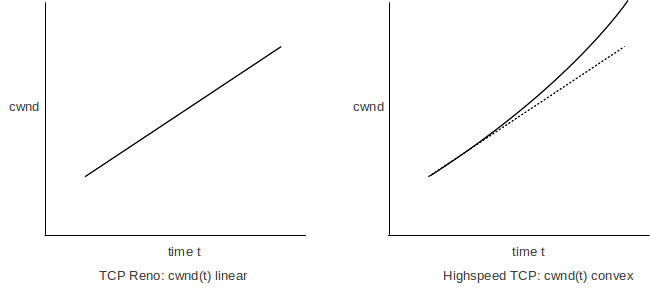
This might be an appropriate time to point out that in TCP Reno, the cwnd-versus-time graph between losses is actually slightly concave (lying below its tangent). We do get a strictly linear graph if we plot cwnd as a function of the count of elapsed RTTs, but the RTTs are themselves slowly increasing as a function of time once the queue starts filling up. At that point, the cwnd-versus-time graph bends slightly down. If the bottleneck queue capacity matches the total path transit capacity, the RTTs for a full queue are about double the RTTs for an empty queue.

In general, when Highspeed-TCP competes with a new TCP Reno flow it is N times as aggressive, and grabs N times the bandwidth, where N = N(cwnd). In this it behaves very much like N separate TCP flows, or, more precisely, N separate TCP flows that have all their loss events completely synchronized.

15.4   TCP Vegas

TCP Vegas, introduced in [BP95], is the only new TCP version we consider here that dates from the previous century. The goal was not directly to address the high-bandwidth problem, but rather to improve TCP throughput generally; indeed, in 1995 the high-bandwidth problem had not yet surfaced as a practical concern. The goal of TCP Vegas is essentially to eliminate congestive losses, and to try to keep the bottleneck link 100% utilized at all times, thus improving on TCP Reno’s typical sawtooth-average bottleneck-link utilization of 75% (13.7   TCP and Bottleneck Link Utilization).

TCP Vegas achieves this improvement by, like DECbit, recognizing TCP congestion at the knee, that is, at the point where the bottleneck link becomes saturated and further cwnd increases simply result in RTT increases. A TCP Vegas sender alone or in competition only with other TCP Vegas connections will seldom if ever approach the “cliff” where packet losses occur.

To accomplish this, no special router cooperation – or even receiver cooperation – is necessary. Instead, the sender uses careful monitoring of the RTT to keep track of the number of “extra packets” (ie packets sitting in queues) it has injected into the network. In the absence of competition, the RTT will remain constant, equal to RTT_noLoad, until cwnd has increased to the point when the bottleneck link has become saturated and the queue begins to fill (6.3.2   RTT Calculations). By monitoring the bandwidth as well, a TCP sender can even determine the actual number of packets in the bottleneck queue, as bandwidth × (RTT − RTT_noLoad). TCP Vegas uses this information to attempt to maintain at all times a small but positive number of packets in the bottleneck queue.

A TCP sender can easily measure available bandwidth; the simplest measurement is cwnd/RTT (measured in packets/sec). Let us denote this bandwidth estimate by BWE; for the time being we will accept BWE as accurate, though see 15.6.1   ACK Compression and Westwood+ below. TCP Vegas estimates RTT_noLoad by the minimum RTT (RTT_min) encountered during the connection. The “ideal” cwnd that just saturates the bottleneck link is BWE×RTT_noLoad. Note that BWE will be much more volatile than RTT_min; the latter will typically reach its final value early in the connection, while BWE will fluctuate up and down with congestion (which will also act on RTT, but by increasing it).

As in 6.3.2   RTT Calculations, any TCP sender can estimate queue utilization as

queue_use = cwnd − BWE×RTT_noLoad = cwnd × (1 − RTT_noLoad/RTT_actual)

TCP Vegas then adjusts cwnd regularly to maintain the following:

𝛼 ≤ queue_use ≤ 𝛽

which is the same as

BWE×RTT_noLoad + 𝛼 ≤ cwnd ≤ BWE×RTT_noLoad + 𝛽

Typically 𝛼 = 2-3 packets and 𝛽 = 4-6 packets. We increment cwnd by 1 if cwnd falls below the lower limit (eg if BWE has increased). Similarly, we decrement cwnd by 1 if BWE drops and cwnd exceeds BWE×RTT_noLoad + 𝛽. These adjustments are conceptually done once per RTT. Typically a TCP Vegas sender would also set cwnd = cwnd/2 if a packet were actually lost, though this does not necessarily happen nearly as often as with TCP Reno.

TCP Vegas achieves its goal quite well. If one monitors the number of packets in queues, through real measurement or in simulation, the number does indeed stay between 𝛼 and 𝛽. In the absence of competition from TCP Reno, a single TCP Vegas connection will never experience congestive packet loss. This is a remarkable achievement.

The use of returning ACKs to determine BWE is subject to errors due to “ACK compression”, 15.6.1   ACK Compression and Westwood+. This is generally not a major problem with TCP Vegas, however.

15.4.1   TCP Vegas versus TCP Reno

Despite its striking ability to avoid congestive losses in the absence of competition, TCP Vegas encounters a potentially serious fairness problem when competing with TCP Reno, at least for the case when queue capacity exceeds or is close to the transit capacity (13.7   TCP and Bottleneck Link Utilization). TCP Vegas will try to minimize its queue use, while TCP Reno happily fills the queue. And whoever has more packets in the queue has a greater share of bandwidth.

To make this precise, suppose we have two TCP connections sharing a bottleneck router R, the first using TCP Vegas and the second using TCP Reno. Suppose further that both connections have a path transit capacity of 10 packets, and R’s queue capacity is 40 packets. If 𝛼=3 and 𝛽=5, TCP Vegas might keep an average of four packets in the queue. Unfortunately, TCP Reno then gobbles up most of the rest of the queue space, as follows. There are 40-4 = 36 spaces left in the queue after TCP Vegas takes its quota, and 10 in the TCP Reno connection’s path, for a total of 46. This represents the TCP Reno connection’s network ceiling, and is the point at which TCP Reno halves cwnd; therefore cwnd will vary from 23 to 46 with an average of about 34. Of these 34 packets, if 10 are in transit then 24 are in R’s queue. If on average R has 24 packets from the Reno connection and 4 from the Vegas connection, then the bandwidth available to these connections will also be in this same 6:1 proportion. The TCP Vegas connection will get 1/7 the bandwidth, because it occupies 1/7 the queue, and the TCP Reno connection will take the other 6/7.

To put it another way, TCP Vegas is potentially too “civil” to compete with TCP Reno.

Even worse, Reno’s aggressive queue filling will eventually force the TCP Vegas cwnd to decrease; see Exercise 4 below.

This Vegas-Reno fairness problem is most significant when the queue size is an appreciable fraction of the path transit capacity. During periods when the queue is empty, TCPs Vegas and Reno increase cwnd at the same rate, so when the queue size is small compared to the path capacity, as is the case for most high-bandwidth paths, TCP Vegas and TCP Reno are much closer to being fair.

In 16.5   TCP Reno versus TCP Vegas we compare TCP Vegas with TCP Reno in actual simulation. With a transit capacity of 220 packets and a queue capacity of 10 packets, TCPs Vegas and Reno receive almost exactly the same bandwidth.

Note that if the bottleneck router used Fair Queuing (to be introduced in 17.5   Fair Queuing) on a per-connection basis, then the TCP Reno connection’s queue greediness would not be of any benefit, and both connections would get similar shares of bandwidth with the TCP Vegas connection experiencing lower delay.

Let us next consider how TCP Vegas behaves when there is an increase in RTT due to the kind of cross traffic shown in 14.2.4   Example 4: cross traffic and RTT variation and again in the diagram below. Let A–B be the TCP Vegas connection and assume that its queue-size target is 4 packets (eg 𝛼=3, 𝛽=5). We will also assume that the RTT_noLoad for the A–B path is about 5ms and the RTT for the C–D path is also low. As before, the link labels represent bandwidths in packets/ms, meaning that the round-trip A–B transit capacity is 10 packets.

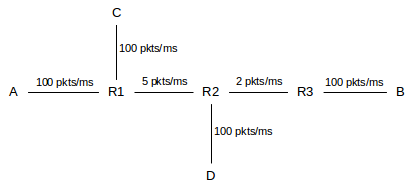
Initially, in the absence of C–D traffic, the A–B connection will send at a rate of 2 packets/ms (the R2–R3 bottleneck), and maintain a queue of four packets at R2. Because the RTT transit capacity is 10 packets, this will be achieved with a window size of 10+4 = 14.

Now let the C–D traffic start up, with a winsize so as to keep about four times as many packets in R1’s queue as A, once the new steady-state is reached. If all four of the A–B connection’s “queue” packets end up now at R1 rather than R2, then C would need to contribute at least 16 packets. These 16 packets will add a delay of about 16/5 ≃ 3ms; the A–B path will see a more-or-less-fixed 3ms increase in RTT. A will also see a decrease in bandwidth due to competition; with C consuming 80% of R1’s queue, A’s share wll fall to 20% and thus its bandwidth will fall to 20% of the R1–R2 link bandwidth, that is, 1 packet/ms. Denote this new value by BWE_new. TCP Vegas will attempt to decrease cwnd so that

cwnd ≃ BWE_new×RTT_noLoad + 4

A’s estimate of RTT_noLoad, as RTT_min, will not change; the RTT has gotten larger, not smaller. So we have BWE_new×RTT_noLoad ≃ 1 packet/ms × 5 ms = 5 packets; adding the 4 reserved for the queue, the new value of cwnd is now about 9, down from 14.

On the one hand, this new value of cwnd does represent 5 packets now in transit, plus 4 in R1’s queue; this is indeed the correct response. But note that this division into transit and queue packets is an average. The actual physical A–B round-trip transit capacity remains about 10 packets, meaning that if the new packets were all appropriately spaced then none of them might be in any queue.

15.5   FAST TCP

FAST TCP is closely related to TCP Vegas; the idea is to keep the fixed-queue-utilization feature of TCP Vegas to the extent possible, but to provide overall improved performance, in particular in the face of competition with TCP Reno. Details can be found in [JWL04] and [WJLH06]. FAST TCP is patented; see patent 7,974,195.

As with TCP Vegas, the sender estimates RTT_noLoad as RTT_min. At regular short fixed intervals (eg 20ms) cwnd is updated via the following weighted average:

cwnd_new = (1-𝛾)×cwnd + 𝛾×((RTT_noLoad/RTT)×cwnd + 𝛼)

where 𝛾 is a constant between 0 and 1 determining how “volatile” the cwnd update is (𝛾≃1 is the most volatile) and 𝛼 is a fixed constant, which, as we will verify shortly, represents the number of packets the sender tries to keep in the bottleneck queue, as in TCP Vegas. Note that the cwnd update frequency is not tied to the RTT.

If RTT is constant for multiple consecutive update intervals, and is larger than RTT_noLoad, the above will converge to a constant cwnd, in which case we can solve for it. Convergence implies cwnd_new = cwnd = ((RTT_noLoad/RTT)×cwnd + 𝛼), and from there we get cwnd×(RTT−RTT_noLoad)/RTT = 𝛼. As we saw in 6.3.2   RTT Calculations, cwnd/RTT is the throughput, and so 𝛼 = throughput × (RTT−RTT_noLoad) is then the number of packets in the queue. In other words, FAST TCP, when it reaches a steady state, leaves 𝛼 packets in the queue. As long as this is the case, the queue will not overflow (assuming 𝛼 is less than the queue capacity).

Whenever the queue is not full, though, we have RTT = RTT_noLoad, in which case FAST TCP’s cwnd-update strategy reduces to cwnd_new = cwnd + 𝛾×𝛼. For 𝛾=0.5 and 𝛼=10, this increments cwnd by 5. Furthermore, FAST TCP performs this increment at a specific rate independent of the RTT, eg every 20ms; for long-haul links this is much less than the RTT. FAST TCP will, in other words, increase cwnd very aggressively until the point when queuing delays occur and RTT begins to increase.

When FAST TCP is competing with TCP Reno, it does not directly address the queue-utilization competition problem experienced by TCP Vegas. FAST TCP will try to limit its queue utilization to 𝛼; TCP Reno, however, will continue to increase its cwnd until the queue is full. Once the queue begins to fill, TCP Reno will pull ahead of FAST TCP just as it did with TCP Vegas. However, FAST TCP does not reduce its cwnd in the face of TCP Reno competition as quickly as TCP Vegas.

However, FAST TCP can often offset this Reno-competition problem in other ways. First, the value of 𝛼 can be increased from the value of around 4 packets originally proposed for TCP Vegas; in [TWHL05] the value 𝛼=30 is suggested. Second, for high bandwidth×delay products, the queue-filling phase of a TCP Reno sawtooth (see 13.7   TCP and Bottleneck Link Utilization) becomes relatively smaller. In the earlier link-unsaturated phase of each sawtooth, TCP Reno increases cwnd by 1 each RTT. As noted above, however, FAST TCP is allowed to increase cwnd much more rapidly in this earlier phase, and so FAST TCP can get substantially ahead of TCP Reno. It may fall back somewhat during the queue-filling phase, but overall the FAST and Reno flows may compete reasonably fairly.

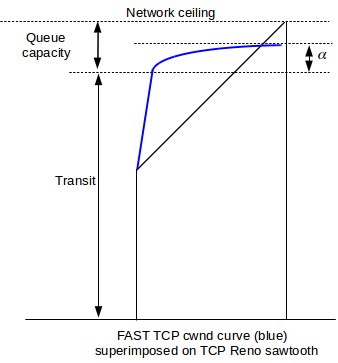
The diagram above illustrates a FAST TCP graph of cwnd versus time, in blue; it is superimposed over one sawtooth of TCP Reno with the same network ceiling. Note that cwnd rises rapidly when it is below the path transit capacity, and then levels off sharply.

15.6   TCP Westwood

TCP Westwood represents an attempt to use the RTT-monitoring strategies of TCP Vegas to address the high-bandwidth problem; recall that the issue there is to distinguish between congestive and non-congestive losses. TCP Westwood can also be viewed as a refinement of TCP Reno’s cwnd=cwnd/2 strategy, which is a greater drop than necessary if the queue capacity at the bottleneck router is less than the transit capacity.

As in TCP Vegas, the sender keeps a continuous estimate of bandwidth, BWE, and estimates RTT_noLoad by RTT_min. The minimum window size to keep the bottleneck link busy is, again as in TCP Vegas, BWE × RTT_noLoad. In TCP Vegas, BWE was calculated as cwnd/RTT; we will continue to use this for the time being but in fact TCP Westwood has used a wide variety of other algorithms, some of which are discussed in the following subsection, to infer the available average bandwidth from the returning ACKs.

The core TCP Westwood innovation is to, on loss, reduce cwnd as follows:

cwnd = max(cwnd/2, BWE×RTT_noLoad)

The product BWE×RTT_noLoad represents what the sender believes is its current share of the “transit capacity” of the path. While BWE may be markedly reduced in the presence of competing traffic, BWE×RTT_noLoad represents how many packets can be in transit (rather than in queues) at the current bandwidth BWE. A TCP Westwood sender never drops cwnd below what it believes to be the current transit capacity for the path.

Consider again the classic TCP Reno sawtooth behavior:

• cwnd alternates between cwnd_min and cwnd_max = 2×cwnd_min.
• cwnd_max ≃ transit_capacity + queue_capacity (or at least the sender’s share of these)

As we saw in 13.7   TCP and Bottleneck Link Utilization, if transit_capacity < cwnd_min, then Reno does a pretty good job keeping the bottleneck link saturated. However, if transit_capacity > cwnd_min, then when Reno drops to cwnd_min, the bottleneck link is not saturated until cwnd climbs to transit_capacity.

Westwood, on the other hand, would in that situation reduce cwnd only to transit_capacity, a smaller reduction. Thus TCP Westwood potentially better handles a wide range of router queue capacities. For bottleneck routers where the queue capacity is small compared to the transit capacity, TCP Westwood would have a higher, finer-pitched sawtooth than TCP Reno: the teeth would oscillate between the network ceiling (= queue+transit) and the transit_capacity, versus Reno’s oscillation between the network ceiling and half the ceiling.

In the event of a non-congestive (noise-related) packet loss, if it happens that cwnd is less than transit_capacity then TCP Westwood does not reduce the window size at all. That is, non-congestive losses with cwnd < transit_capacity have no effect. When cwnd > transit_capacity, losses reduce cwnd only to transit_capacity, and thus the link stays saturated.

In the large-cwnd, high-bandwidth case, non-congestive packet losses can easily lower the TCP Reno cwnd to well below what is necessary to keep the bottleneck link saturated. In TCP Westwood, on the other hand, the average cwnd may be lower than it would be without the non-congestive losses, but it will be high enough to keep the bottleneck link saturated.

TCP Westwood uses BWE×RTT_noLoad as a floor for reducing cwnd. TCP Vegas shoots to have the actual cwnd be just a few packets above this.

TCP Westwood is not any more aggressive than TCP Reno at increasing cwnd in no-loss situations. So while it handles the non-congestive-loss part of the high-bandwidth TCP problem very well, it does not particularly improve the ability of a sender to take advantage of a sudden large rise in the network ceiling.

TCP Westwood is also potentially very effective at addressing the lossy-link problem, as most non-congestive losses would result in no change to cwnd.

15.6.1   ACK Compression and Westwood+

So far, we have been assuming that ACKs never encounter queuing delays. They in fact will not, if they are traveling in the reverse direction from all data packets. But while this scenario covers any single-sender model and also systems of two or more competing senders, real networks have more complicated traffic patterns, and returning ACKs from an A⟶B data flow can indeed experience queuing delays if there is third-party traffic along some link in the B⟶A path.

Delay in the delivery of ACKs, leading to clustering of their arrival, is known as ACK compression; see [ZSC91] and [JM92] for examples. ACK compression causes two problems. First, arriving clusters of ACKs trigger corresponding bursts of data transmissions in sliding-windows senders; the end result is an uneven data-transmission rate. Normally the bottleneck-router queue can absorb an occasional burst; however, if the queue is nearly full such bursts can lead to premature or otherwise unexpected losses.

The second problem with late-arriving ACKs is that they can lead to inaccurate or fluctuating measurements of bandwidth, upon which both TCP Vegas and TCP Westwood depend. For example, if bandwidth is estimated as cwnd/RTT, late-arriving ACKs can lead to inaccurate calculation of RTT. The original TCP Westwood strategy was to estimate bandwidth from the spacing between consecutive ACKs, much as is done with the packet-pairs technique (14.2.6   Packet Pairs) but smoothed with a suitable running average. This strategy turned out to be particularly vulnerable to ACK-compression errors.

For TCP Vegas, ACK compression means that occasionally the sender’s cwnd may fail to be decremented by 1; this does not appear to be a significant impact, perhaps because cwnd is changed by at most ±1 each RTT. For Westwood, however, if ACK compression happens to be occurring at the instant of a packet loss, then a resultant transient overestimation of BWE may mean that the new post-loss cwnd is too large; at a point when cwnd was supposed to fall to the transit capacity, it may fail to do so. This means that the sender has essentially taken a congestion loss to be non-congestive, and ignored it. The influence of this ignored loss will persist – through the much-too-high value of cwnd – until the following loss event.

To fix these problems, TCP Westwood has been amended to Westwood+, by increasing the time interval over which bandwidth measurements are made and by inclusion of an averaging mechanism in the calculation of BWE. Too much smoothing, however, will lead to an inaccurate BWE just as surely as too little.

Suitable smoothing mechanisms are given in [FGMPC02] and [GM03]; the latter paper in particular examines several smoothing algorithms in terms of their resistance to aliasing effects: the tendency for intermittent measurement of a periodic signal (the returning ACKs) to lead to much greater inaccuracy than might initially be expected. One smoothing filter suggested by [GM03] is to measure BWE only over entire RTTs, and then to keep a cumulative running average as follows, where BWM_k is the measured bandwidth over the kth RTT:

BWE_k = 𝛼×BWE_k-1 + (1−𝛼)×BWM_k

A suggested value of 𝛼 is 0.9.

15.7   TCP Veno

TCP Veno ([FL03]) is a synthesis of TCP Vegas and TCP Reno, which attempts to use the RTT-monitoring ideas of TCP Vegas while at the same time remaining about as “aggressive” as TCP Reno in using queue capacity. TCP Veno has generally been presented as an option to address TCP’s lossy-link problem, rather than the high-bandwidth problem per se.

A TCP Veno sender estimates the number N of packets likely in the bottleneck queue as N_queue = cwnd - BWE×RTT_noLoad, like TCP Vegas. TCP Veno then modifies the TCP Reno congestion-avoidance rule as follows, where the parameter 𝛽, representing the queue-utilization value at which TCP Veno slows down, might be around 5.

if N_queue<𝛽, cwnd = cwnd + 1 each RTT

if N_queue≥𝛽, cwnd = cwnd + 0.5 each RTT

The above strategy makes cwnd growth less aggressive once link saturation is reached, but does continue to increase cwnd (half as fast as TCP Reno) until the queue is full and congestive losses occur.

When a packet loss does occur, TCP Veno uses its current value of N_queue to attempt to distinguish between non-congestive and congestive loss, as follows:

if N_queue<𝛽, the loss is probably not due to congestion; set cwnd = (4/5)×cwnd

if N_queue≥𝛽, the loss probably is due to congestion; set cwnd = (1/2)×cwnd as usual

The idea here is that most router queues will have a total capacity much larger than 𝛽, so a loss with fewer than 𝛽 likely does not represent a queue overflow. Note that, by comparison, TCP Westwood leaves cwnd unchanged if it thinks the loss is not due to congestion, and its threshold for making that determination is N_queue=0.

If TCP Veno encounters a series of non-congestive losses, the above rules make it behave like AIMD(1,0.8). Per the analysis in 14.7   AIMD Revisited, this is equivalent to AIMD(2,0.5); this means TCP Veno will be about twice as aggressive as TCP Reno in recovering from non-congestive losses. This would provide a definite improvement in lossy-link situations with modest bandwidth×delay products, but may not be enough to make a major dent in the high-bandwidth problem.

15.8   TCP Hybla

TCP Hybla ([CF04]) has one very specific focus: to address the TCP satellite problem (3.5.2   Satellite Internet) of very long RTTs. TCP Hybla selects a more-or-less arbitrary “reference” RTT, called RTT₀, and attempts to scale TCP Reno so as to behave like a TCP Reno connection with an RTT of RTT₀. In the paper [CF04] the authors suggest RTT₀ = 25ms.

Suppose a TCP Reno connection has at a loss event at time t₀ reduced cwnd to cwnd_min. TCP Reno will then increment cwnd by 1 for each RTT, until the next loss event. This Reno behavior can be equivalently expressed in terms of the current time t as follows:

cwnd = (t−t₀)/RTT + cwnd_min

What TCP Hybla does is to use the above formula after replacing the actual RTT (or RTT_noLoad) with RTT₀. Equivalently, TCP Hybla defines the ratio of the two RTTs as 𝜌 = RTT/RTT₀, and then after each windowful (each time interval of length RTT) increments cwnd by 𝜌² instead of by 1. In the event that RTT < RTT₀, 𝜌 is set to 1, so that short-RTT connections are not penalized.

Because cwnd now increases each RTT by 𝜌², which can be relatively large, there is a good chance that when the network ceiling is reached there will be a burst of losses of size ~𝜌². Therefore, TCP Hybla strongly recommends that the receiving end support SACK TCP, so as to allow faster recovery from multiple packet losses. Another recommended feature is the use of TCP Timestamps; this is a standard TCP option that allows the sender to include its own timestamp in each data packet. The receiver is to echo back the timestamp in the corresponding ACK, thus allowing more accurate measurement by the receiver of the actual RTT. Finally, to further avoid having these relatively large increments to cwnd result in multiple packet losses, TCP Hybla recommends some form of “pacing” to smooth out the actual transmission times. Rather than sending out four packets upon receipt of an ACK, for example, we might estimate the time T to the next transmission batch (eg when the next ACK arrives) and send the packets at intervals of T/4.

TCP Hybla applies a similar 𝜌-fold scaling mechanism to threshold slow start, when a value for ssthresh is known. But the initial unbounded slow start is much more difficult to scale. Scaling at that point would mean repeatedly doubling cwnd and sending out flights of packets, before any ACKs have been received; this would likely soon lead to congestive collapse.

15.9   TCP Illinois

The general idea behind TCP Illinois, described in [LBS06], is to use the usual AIMD(𝛼,𝛽) strategy but to have 𝛼 = 𝛼(RTT) be a decreasing function of the current RTT, rather than a constant. When the queue is empty and RTT is equal to RTT_noLoad, then 𝛼 will be large, and cwnd will increase rapidly. Once RTT starts to increase, however, 𝛼 will decrease rapidly, and the cwnd growth will level off. This leads to the same kind of concave cwnd graph as we saw above in FAST TCP; a consequence of this is that for most of the time between consecutive loss events cwnd is large enough to keep the bottleneck link close to saturated, and so to keep throughput high.

The actual 𝛼() function is not of RTT, but rather of delay, defined to be RTT − RTT_noLoad. As with TCP Vegas, RTT_noLoad is estimated by RTT_min. As a connection progresses, the sender maintains continually updated values not only for RTT_min but also for RTT_max. The sender then sets delay_max to be RTT_max − RTT_min.

We are now ready to define 𝛼(delay). We first specify the highest value of 𝛼, 𝛼_max, and the lowest, 𝛼_min. In [LBS06] these are 10.0 and 0.1 respectively; in my linux 3.5 kernel they are 10.0 and 0.3. We also define delay_thresh to be 0.01×delay_max (the 0.01 is another tunable parameter). We then define 𝛼(delay) as follows

𝛼(delay) = 𝛼_max if delay ≤ delay_thresh

𝛼(delay) = k₁/(delay+k₂) if delay_thresh ≤ delay ≤ delay_max

where k₁ and k₂ are chosen so that, for the lower formula, 𝛼(delay_thresh) = 𝛼_max and 𝛼(delay_max) = 𝛼_min. In case there is a sudden spike in delay, delay_max is updated before the above is evaluated, so we always have delay ≤ delay_max. Here is a graph:

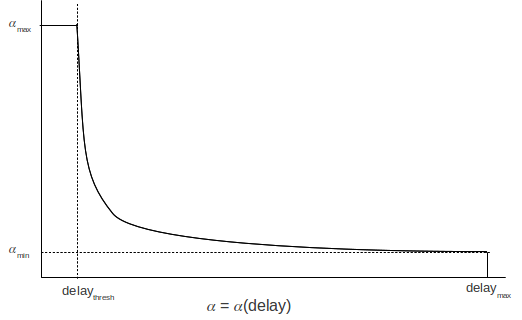
Whenever RTT = RTT_noLoad, delay=0 and so 𝛼(delay) = 𝛼_max. However, as soon as queuing delay just barely starts to begin, we will have delay > delay_thresh and so 𝛼(delay) begins to fall – rather precipitously – to 𝛼_min. The value of 𝛼(delay) is always positive, though, so cwnd will continue to increase (unlike TCP Vegas) until a congestive loss eventually occurs. However, at that point the change in cwnd is very small, which minimizes the probability that multiple packets will be lost.

Note that, as with FAST TCP, the increase in delay is used to trigger the reduction in 𝛼.

TCP Illinois also supports having 𝛽 be a decreasing function of delay, so that 𝛽(small_delay) might be 0.2 while 𝛽(larger_delay) might match TCP Reno’s 0.5. However, the authors of [LBS06] explain that “the adaptation of 𝛽 as a function of average queuing delay is only relevant in networks where there are non-congestion-related losses, such as wireless networks or extremely high speed networks”.

15.10   H-TCP

H-TCP, or TCP-Hamilton, is described in [LSL05]. Like Highspeed-TCP it primarily allows for faster growth of cwnd; unlike Highspeed-TCP, the cwnd increment is determined not by the size of cwnd but by the elapsed time since the previous loss event. The threshold for accelerated cwnd growth is generally set to be 1.0 seconds after the most recent loss event. Using an RTT of 50 ms, that amounts to 20 RTTs, suggesting that when cwnd_min is less than 20 then H-TCP behaves very much like TCP Reno.

The specific H-TCP acceleration rule first defines a time threshold t_L. If t is the elapsed time in seconds since the previous loss event, then for t≤t_L the per-RTT window-increment 𝛼 is 1. However, for t>t_L we define

𝛼(t) = 1 + 10(t−t_L) + (t−t_L)²/4

We then increment cwnd by 𝛼(t) after each RTT, or, equivalently, by 𝛼(t)/cwnd after each received ACK.

At t=t_L+1 seconds (nominally 2 seconds), 𝛼 is 12. The quadratic term dominates the linear term when t−t_L > 40. If RTT = 50 ms, that is 800 RTTs.

Even if cwnd is very large, growth is at the same rate as for TCP Reno until t>t_L; one consequence of this is that, at least in the first second after a loss event, H-TCP competes fairly with TCP Reno, in the sense that both increase cwnd at the same absolute rate. H-TCP starts “from scratch” after each packet loss, and does not re-enter its “high-speed” mode, even if cwnd is large, until after time t_L.

A full H-TCP implementation also adjusts the multiplicative factor 𝛽 as follows (the paper [LSL05] uses 𝛽 to represent what we denote by 1−𝛽). The RTT is monitored, as with TCP Vegas. However, the RTT increase is not used for per-packet or per-RTT adjustments; instead, these measurements are used after each loss event to update 𝛽 so as to have

1−𝛽 = RTT_min/RTT_max

The value 1−𝛽 is capped at a maximum of 0.8, and at a minimum of 0.5. To see where the ratio above comes from, first note that RTT_min is the usual stand-in for RTT_noLoad, and RTT_max is, of course, the RTT when the bottleneck queue is full. Therefore, by the reasoning in 6.3.2   RTT Calculations, equation 5, 1−𝛽 is the ratio transit_capacity / (transit_capacity + queue_capacity). At a congestion event involving a single uncontested flow we have cwnd = transit_capacity + queue_capacity, and so after reducing cwnd to (1−𝛽)×cwnd, we have cwnd_new = transit_capacity, and hence (as in 13.7   TCP and Bottleneck Link Utilization) the bottleneck link will remain 100% utilized after a loss. The cap on 1−𝛽 of 0.8 means that if the queue capacity is smaller than a quarter of the transit capacity then the bottleneck link will experience some idle moments.

When 𝛽 is changed, H-TCP also adjusts 𝛼 to 𝛼ʹ = 2𝛽𝛼(t) so as to improve fairness with other H-TCP connections with different current values of 𝛽.

15.11   TCP CUBIC

TCP Cubic attempts, like Highspeed TCP, to solve the problem of efficient TCP transport when bandwidth×delay is large. TCP Cubic allows very fast window expansion; however, it also makes attempts to slow the growth of cwnd sharply as cwnd approaches the current network ceiling, and to treat other TCP connections fairly. Part of TCP Cubic’s strategy to achieve this is for the window-growth function to slow down (become concave) as the previous network ceiling is approached, and then to increase rapidly again (become convex) if this ceiling is surpassed without losses. This concave-then-convex behavior mimics the graph of the cubic polynomial cwnd = t³, hence the name (TCP Cubic also improves an earlier TCP version known as TCP BIC).

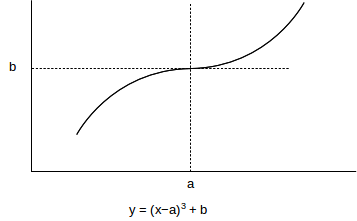
As mentioned above, TCP Cubic is currently (2013) the default linux congestion-control implementation. TCP Cubic is documented in [HRX08]. TCP Cubic is not described in an RFC, but there is an Internet Draft http://tools.ietf.org/id/draft-rhee-tcpm-cubic-02.txt.

TCP Cubic has a number of interrelated features, in an attempt to address several TCP issues:

• Reduction in RTT bias
• TCP Friendliness when most appropriate
• Rapid recovery of cwnd following its decrease due to a loss event, maximizing throughput
• Optimization for an unchanged network ceiling (corresponding to cwnd_max)
• Rapid expansion of cwnd when a raised network ceiling is detected

The eponymous cubic polynomial y=x³, appropriately shifted and scaled, is used to determine changes in cwnd. No special algebraic properties of this polynomial are used; the point is that the curve, while steadily increasing, is first concave and then convex; the authors of [HRX08] write “[t]he choice for a cubic function is incidental and out of convenience”. This y=x³ polynomial has an inflection point at x=0 where the tangent line is horizontal; this is the point where the graph changes from concave to convex.

We start with the basic outline of TCP Cubic and then consider some of the bells and whistles. We assume a loss has just occurred, and let W_max denote the value of cwnd at the point when the loss was discovered. TCP Cubic then sets cwnd to 0.8×W_max; that is, TCP Cubic uses 𝛽 = 0.2. The corresponding 𝛼 for TCP-Friendly AIMD(𝛼,𝛽) would be 𝛼=1/3, but TCP Cubic uses this 𝛼 only in its TCP-Friendly adjustment, below.

We now define a cubic polynomial W(t), a shifted and scaled version of w=t³. The parameter t represents the elapsed time since the most recent loss, in seconds. At time t>0 we set cwnd = W(t). The polynomial W(t), and thus the cwnd rate of increase, as in TCP Hybla, is no longer tied to the connection’s RTT; this is done to reduce if not eliminate the RTT bias that is so deeply ingrained in TCP Reno.

We want the function W(t) to pass through the point representing the cwnd just after the loss, that is, ⟨t,W⟩ = ⟨0,0.8×W_max⟩. We also want the inflection point to lie on the horizontal line y=W_max. To fully determine the curve, it is at this point sufficient to specify the value of t at this inflection point; that is, how far horizontally W(t) must be stretched. This horizontal distance from t=0 to the inflection point is represented by the constant K in the following equation; W(t) returns to its pre-loss value W_max at t=K. C is a second constant.

W(t) = C×(t−K)³ + W_max

It suffices algebraically to specify either C or K; the two constants are related by the equation obtained by plugging in t=0. K changes with each loss event, but it turns out that the value of C can be constant, not only for any one connection but for all TCP Cubic connections. TCP Cubic specifies for C the ad hoc value 0.4; we can then set t=0 and, with a bit of algebra, solve to obtain

K = (W_max/2)^1/3 seconds

If W_max = 250, for example, K=5; if RTT = 100 ms, this is 50 RTTs.

When each ACK arrives, TCP Cubic records the arrival time t, calculates W(t), and sets cwnd = W(t). At the next packet loss the parameters of W(t) are updated.

If the network ceiling does not change, the next packet loss will occur when cwnd again reaches the same W_max; that is, at time t=K after the previous loss. As t approaches K and the value of cwnd approaches W_max, the curve W(t) flattens out, so cwnd increases slowly.

This concavity of the cubic curve, increasing rapidly but flattening near W_max, achieves two things. First, throughput is boosted by keeping cwnd close to the available path transit capacity. In 13.7   TCP and Bottleneck Link Utilization we argued that if the path transit capacity is large compared to the bottleneck queue capacity (and this is the case for which TCP Cubic was designed), then TCP Reno averages 75% utilization of the available bandwidth. The bandwidth utilization increases linearly from 50% just after a loss event to 100% just before the next loss. In TCP Cubic, the initial rapid rise in cwnd following a loss means that the average will be much closer to 100%. Another important advantage of the flattening is that when cwnd is finally incremented to the point of loss, it likely is just over the network ceiling; the connection has an excellent chance that only one or two packets are lost rather than a large burst. This facilitates the NewReno Fast Recovery algorithm, which TCP Cubic still uses if the receiver does not support SACK TCP.

Once t>K, W(t) becomes convex, and in fact begins to increase rapidly. In this region, cwnd > W_max, and so the sender knows that the network ceiling has increased since the previous loss. The TCP Cubic strategy here is to probe aggressively for additional capacity, increasing cwnd very rapidly until the new network ceiling is encountered. The cubic increase function is in fact quite aggressive when compared to any of the other TCP variants discussed here, and time will tell what strategy works best. As an example in which the TCP Cubic approach seems to pay off, let us suppose the current network ceiling is 2,000 packets, and then (because competing connections have ended) increases to 3,000. TCP Reno would take 1,000 RTTs for cwnd to reach the new ceiling, starting from 2,000; if one RTT is 50 ms that is 50 seconds. To find the time t-K that TCP Cubic will need to increase cwnd from 2,000 to 3,000, we solve 3000 = W(t) = C×(t−K)³ + 2000, which works out to t-K ≃ 13.57 seconds (recall 2000 = W(K) here).

The constant C=0.4 is determined empirically. The cubic inflection point occurs at t = K = (W_max×𝛽/C)^1/3. A larger C reduces the time K between the a loss event and the next inflection point, and thus the time between consecutive losses. If W_max = 2000, we get K=10 seconds when 𝛽=0.2 and C=0.4. If the RTT were 50 ms, 10 seconds would be 200 RTTs.

For TCP Reno, on the other hand, the interval between adjacent losses is W_max/2 RTTs. If we assume a specific value for the RTT, we can compare the Reno and Cubic time intervals between losses; for an RTT of 50 ms we get

Wmax	Reno	Cubic
2000	50 sec	10 sec
250	6.2 sec	5 sec
54	1.35 sec	3 sec

For smaller RTTs, the basic TCP Cubic strategy above runs the risk of being at a competitive disadvantage compared to TCP Reno. For this reason, TCP Cubic makes a TCP-Friendly adjustment in the window-size calculation: on each arriving ACK, cwnd is set to the maximum of W(t) and the window size that TCP Reno would compute. The TCP Reno calculation can be based on an actual count of incoming ACKs, or be based on the formula (1-𝛽)×W_max + 𝛼×t/RTT.

Note that this adjustment is only “half-friendly”: it guarantees that TCP Cubic will not choose a window size smaller than TCP Reno’s, but places no restraints on the choice of a larger window size.

A consequence of the TCP-Friendly adjustment is that, on networks with modest bandwidth×delay products, TCP Cubic behaves exactly like TCP Reno.

TCP Cubic also has a provision to detect if a given W_max is lower than the previous value, suggesting increasing congestion; in this situation, cwnd is lowered by an additional factor of 1−𝛽/2. This is known as fast convergence, and helps TCP Cubic adapt more quickly to reductions in available bandwidth.

The following graph is taken from [RX05], and shows TCP Cubic connections competing with each other and with TCP Reno.

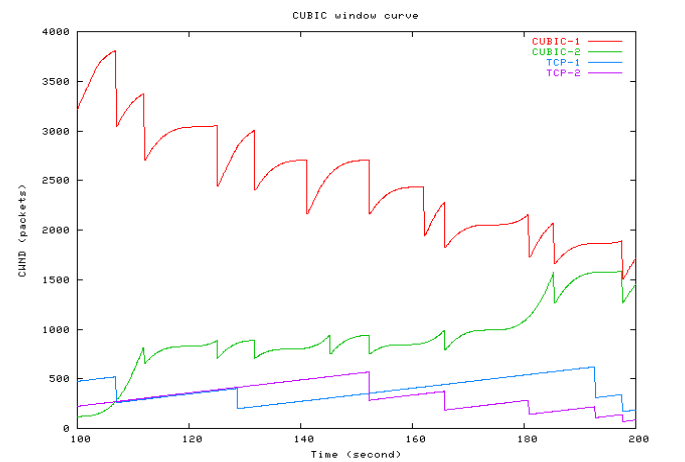
The diagram shows four connections, all with the same RTT. Two are TCP Cubic and two are TCP Reno. The red connection, cubic-1, was established and with a maximum cwnd of about 4000 packets when the other three connections started. Over the course of 200 seconds the two TCP Cubic connections reach a fair equilibrium; the two TCP Reno connections reach a reasonably fair equilibrium with one another, but it is much lower than that of the TCP Cubic connections.

On the other hand, here is a graph from [LSM07], showing the result of competition between two flows using an earlier version of TCP Cubic over a low-speed connection. One connection has an RTT of 160ms and the other has an RTT a tenth that. The bottleneck bandwidth is 1 Mbit/sec, meaning that the bandwidth×delay product for the 160ms connection is 13-20 packets (depending on the packet size used).

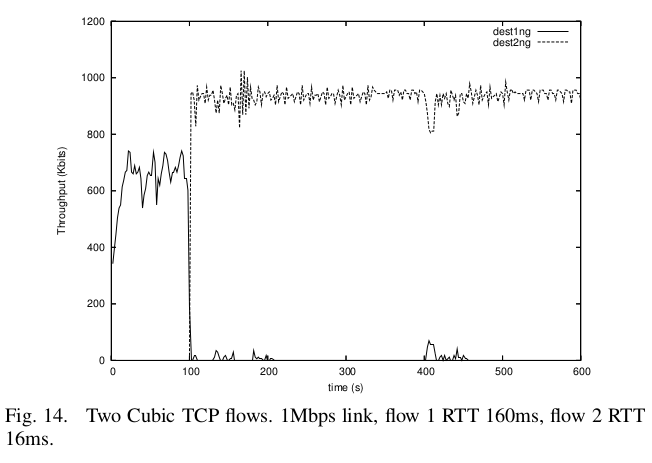
Note that the longer-RTT connection (the solid line) is almost completely starved, once the shorter-RTT connection starts up at T=100. This is admittedly an extreme case, and there have been more recent fixes to TCP Cubic, but it does serve as an example of the need for testing a wide variety of competition scenarios.

15.12   Epilog

TCP Reno’s core congestion algorithm is based on algorithms in Jacobson and Karel’s 1988 paper [JK88], now twenty-five years old. There are concerns both that TCP Reno uses too much bandwidth (the greediness issue) and that it does not use enough (the high-bandwidth-TCP problem).

There are also broad changes in TCP usage patterns. Twenty years ago, the vast majority of all TCP traffic represented downloads from “major” servers. Today, over half of all Internet TCP traffic is peer-to-peer rather than server-to-client. The rise in online video streaming creates new demands for excellent TCP real-time performance.

So which TCP version to use? That depends on circumstances; some of the TCPs above are primarily intended for relatively specific environments; for example, TCP Hybla for satellite links and TCP Veno for mobile devices (including wireless laptops). If the sending and receiving hosts are under common management, and especially if intervening traffic patterns are relatively stable, one can simply make sure the receiver has what it needs for optimum performance (eg SACK TCP) and run a few simple experiments to find what works best.

That leaves the question of what TCP to use on a server that is serving up large volumes of data, perhaps to a range of disparate hosts and with a wide variety of competing-traffic scenarios. Experimentation works here too, but likely with a much larger number of trials. There is also the possibility that one eventually finds a solution that works well, only to discover that it succeeds at the expense of other, competing traffic. These issues suggest a need for continued research into how to update and improve TCP, and Internet congestion-management generally.

Finally, while most new TCPs are designed to hold their own in a Reno world, there is some question that perhaps we would all be better off with a radical rather than incremental change. Might TCP Vegas be a better choice, if only the queue-grabbing greediness of TCP Reno could be restrained? Questions like these are today entirely hypothetical, but it is not impossible to envision an Internet backbone that implemented non-FIFO queuing mechanisms (17   Queuing and Scheduling) that fundamentally changed the rules of the game.

15.13   Exercises

1. How would TCP Vegas respond if it estimated RTT_noLoad = 100ms, with a bandwidth of 1 packet/ms, and then due to a routing change the RTT_noLoad increased to 200ms without changing the bandwidth? What cwnd would be chosen? Assume no competition from other senders.

2. Suppose a TCP Vegas connection from A to B passes through a bottleneck router R. The RTT_noLoad is 50 ms and the bottleneck bandwidth is 1 packet/ms.

(a). If the connection keeps 4 packets in the queue (eg 𝛼=3, 𝛽=5), what will RTT_actual be? What value of cwnd will the connection choose? What will be the value of BWE?

(b). Now suppose a competing (non-Vegas) connection keeps 6 packets in the queue to the Vegas connection’s 4, eventually meaning that the other connection will have 60% of the bandwidth. What will be the Vegas connection’s steady-state values for RTT_actual, cwnd and BWE?

3. Suppose a TCP Vegas connection has R as its bottleneck router. The transit capacity is M, and the queue utilization is currently Q>0 (meaning that the transit path is 100% utilized, although not necessarily by the TCP Vegas packets). The current TCP Vegas cwnd is cwnd_V. Show that the number of packets TCP Vegas calculates are in the queue, queue_use, is

queue_use = cwnd_V×Q/(Q+M)

4. Suppose that at time T=0 a TCP Vegas connection and a TCP Reno connection share the same path, and each has 100 packets in the bottleneck queue, exactly filling the transit capacity of 200. TCP Vegas uses 𝛼=1, 𝛽=2. By the previous exercise, in any RTT with cwnd_V TCP Vegas packets and cwnd_R TCP Reno packets in flight and cwnd_V+cwnd_R>200, N_queue is cwnd_V/(cwnd_V+cwnd_R) multiplied by the total queue utilization cwnd_V+cwnd_R−200.

Continue the following table, where T is measured in RTTs, up through the next two RTTs where cwnd_V is not decremented; that is, find the next two rows where the TCP Vegas queue share is less than 2. (After each of these RTTs, cwnd_V is not decremented.) This can be done either with a spreadsheet or by simple algebra. Note that the TCP Reno cwnd_R will always increment.

T	cwndV	cwndR	TCP Vegas queue share
0	100	100	0
1	101	101	1
2	102	102	2
3	101	103	(101/204)x4 = 1.980 < 𝛽
4	101	104	Vegas has (101/205)×5 = 2.463 packets in queue
5	100	105	Vegas has (100/205)×5 = 2.435 packets in queue
6	99	106	(99/205)×5 = 2.439

This exercise attempts to explain the linear decrease in the TCP Vegas graph in the diagram in 16.5   TCP Reno versus TCP Vegas. Competition with TCP Reno means not only that cwnd_V stops increasing, but in fact it decreases by 1 most RTTs.

5. Suppose that, as in the previous exercise, a FAST TCP connection and a TCP Reno connection share the same path, and at T=0 each has 100 packets in the bottleneck queue, exactly filling the transit capacity of 200. The FAST TCP parameter 𝛾 is 0.5. The FAST TCP and TCP Reno connections have respective cwnds of cwnd_F and cwnd_R. You may use the fact that, as long as the queue is nonempty, RTT/RTT_noLoad = (cwnd_F+|R2|)/200.

Find the value of cwnd_F at T=40, where T is counted in units of 20 ms until T = 40, using 𝛼=4, 𝛼=10 and 𝛼=30. Assume RTT ≃ 20 ms as well. Use of a spreadsheet is recommended. The table here uses 𝛼=10.

T	cwndF	cwndR
0	100	100
1	105	101
2	108.47	102
3	110.77	103
4	112.20	104

6. Suppose A sends to B as in the layout below. The packet size is 1 KB and the bandwidth of the bottleneck R–B link is 1 packet / 10 ms; returning ACKs are thus normally spaced 10 ms apart. The RTT_noLoad for the A–B path is 200 ms.

A───R───B
    │
    C

However, large amounts of traffic are also being sent from C to A; the bottleneck link for that path is R–A with bandwidth 1 KB / 5 ms. The queue at R for the R–A link has a capacity of 40 KB. ACKs are 50 bytes.

(a). What is the maximum possible arrival time difference on the A–B path for ACK[0] and ACK[20], if there are no queuing delays at R in the A→B direction? ACK[0] should be forwarded immediately by R; ACK[20] should have to wait for 40 KB at R

(b). What is the minimum possible arrival time difference for the same ACK[0] and ACK[20]?

7. Suppose a TCP Veno and a TCP Reno connection compete along the same path; there is no other traffic. Both start at the same time with cwnds of 50; the total transit capacity is 160. Both share the next loss event. The bottleneck router’s queue capacity is 60 packets; sometimes the queue fills and at other times it is empty. TCP Veno’s parameter 𝛽 is zero, meaning that it shifts to a slower cwnd increment as soon as the queue just begins filling.

(a). In how many RTTs will the queue begin filling?

(b). At the point the queue is completely filled, how much larger will the Reno cwnd be than the Veno cwnd?

8. Suppose two connections use TCP Hybla. They do not compete. The first connection has an RTT of 100 ms, and the second has an RTT of 1000 ms. Both start with cwnd_min = 0 (literally meaning that nothing is sent the first RTT).

(a). How many packets are sent by each connection in four RTTs (involving three cwnd increases)?

(b). How many packets are sent by each connection in four seconds??

Recall 1+2+3+...+N = N(N+1)/2.

9. Suppose that at time T=0 a TCP Illinois connection and a TCP Reno connection share the same path, and each has 100 packets in the bottleneck queue, exactly filling the transit capacity of 200. The respective cwnds are cwnd_I and cwnd_R. The bottleneck queue capacity is 100.

Find the value of cwnd_I at T=50, where T is the number of elapsed RTTs. At this point cwnd_R is, of course, 150.

T	cwndI	cwndR
0	100	100
1	101	101
2	?	102

You may assume that the delay, RTT − RTT_noLoad, is proportional to queue_utilization = cwnd_I+|R3|−200𝛼. Using this expression to represent delay, delay_max = 100 and so delay_thresh = 1. When calculating 𝛼(delay), assume 𝛼_max = 10 and 𝛼_min = 0.1.

10. Assume that a TCP connection has an RTT of 50 ms, and the time between loss events is 10 seconds.

(a). For a TCP Reno connection, what is the bandwidth×delay product?

(b). For an H-TCP connection, what is the bandwidth×delay product?

11. For each of the values of W_max below, find the change in cwnd over one 100 ms RTT at each of the following points:

i. Immediately after the previous loss event, when t = 0.

ii. At the midpoint of the tooth, when t=K/2

iii. At the point when cwnd has returned to W_max, at t=K

(a). W_max = 250 (making K=5)

(b). W_max = 2000 (making K=10)

12. Suppose a TCP Reno connection is competing with a TCP Cubic connection. There is no other traffic. All losses are synchronized. In this setting, once the steady state is reached, the cwnd graphs for one tooth will look like this:

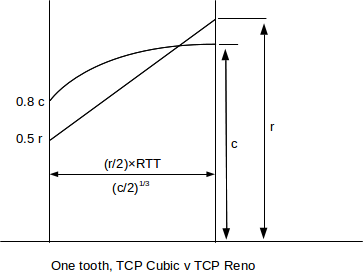
Let c be the maximum cwnd of the TCP Cubic connection (c=W_max) and let r be the maximum of the TCP Reno connection. Let M be the network ceiling, so a loss occurs when c+r reaches M. The width of the tooth for TCP Reno is (r/2)×RTT, where RTT is measured in seconds; the width of the TCP Cubic tooth is (c/2)^1/3. For the examples here, ignore the TCP-Friendly feature of TCP Cubic.

(a). If M = 200 and RTT = 50 ms = 0.05 sec, show that at the steady state r ≃ 130.4 and c = M−r ≃ 69.6.

(b). Find equilibrium r and c (to the nearest integer) for M=1000 and RTT = 50 ms. Hint: use of a spreadsheet or scripting language makes trial-and-error quite practical.

(c). Find equilibrium r and c for M = 1000 and RTT = 100 ms.